How To Normalize Data Of Different Lengths

How to Normalize and Standardize Time Series Data in Python

Last Updated on August 28, 2019

Some machine learning algorithms will accomplish meliorate performance if your time series data has a consequent scale or distribution.

2 techniques that you tin apply to consistently rescale your fourth dimension series data are normalization and standardization.

In this tutorial, you lot volition notice how you tin can apply normalization and standardization rescaling to your time series data in Python.

Later completing this tutorial, you will know:

The limitations of normalization and expectations of your information for using standardization.
What parameters are required and how to manually calculate normalized and standardized values.
How to normalize and standardize your time series data using scikit-learn in Python.

Kick-showtime your projection with my new book Fourth dimension Serial Forecasting With Python, including footstep-past-step tutorials and the Python source code files for all examples.

Let'south go started.

Updated Apr/2019: Updated the link to dataset.
Updated Aug/2019: Updated information loading to apply new API.

How to Normalize and Standardize Fourth dimension Series Data in Python
Photo by Sage Ross, some rights reserved.

Minimum Daily Temperatures Dataset

This dataset describes the minimum daily temperatures over 10 years (1981-1990) in the urban center Melbourne, Australia.

The units are in degrees Celsius and there are 3,650 observations. The source of the data is credited as the Australian Bureau of Meteorology.

Download the dataset.

Below is a sample of the first v rows of data, including the header row.

"Date","Temperatures"

"1981-01-01",20.7

"1981-01-02",17.9

"1981-01-03",eighteen.8

"1981-01-04",14.6

"1981-01-05",15.8

Below is a plot of the entire dataset.

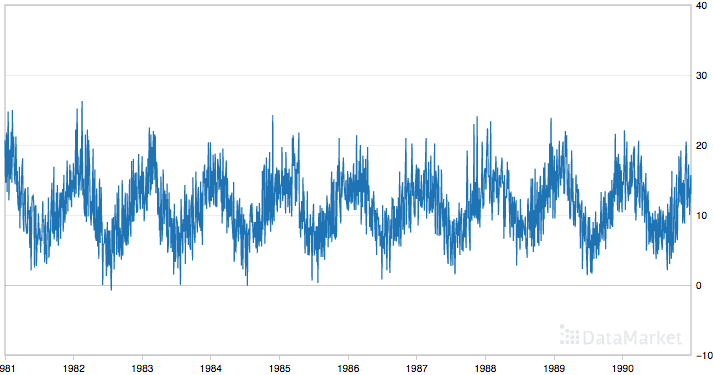
Minimum Daily Temperatures

The dataset shows a strong seasonality component and has a nice, fine-grained detail to work with.

Download the dataset.

This tutorial assumes that the dataset is in your electric current working directory with the filename "daily-minimum-temperatures-in-me.csv".

Stop learning Time Series Forecasting the tedious way!

Accept my free seven-day electronic mail course and discover how to get started (with sample lawmaking).

Click to sign-up and also get a gratis PDF Ebook version of the course.

Normalize Time Series Data

Normalization is a rescaling of the data from the original range and so that all values are within the range of 0 and i.

Normalization can be useful, and fifty-fifty required in some machine learning algorithms when your time series data has input values with differing scales.Information technology may be required for algorithms, like grand-Nearest neighbors, which uses distance calculations and Linear Regression and Artificial Neural Networks that weight input values.

Normalization requires that you know or are able to accurately estimate the minimum and maximum observable values. You may be able to estimate these values from your bachelor data. If your time series is trending up or downward, estimating these expected values may be difficult and normalization may not be the best method to use on your problem.

A value is normalized as follows:

y = (x - min) / (max - min)

Where the minimum and maximum values pertain to the value x being normalized.

For example, for the temperature data, we could guesstimate the min and max observable values every bit 30 and -ten, which are profoundly over and under-estimated. We can then normalize any value like 18.8 as follows:

y = (10 - min) / (max - min)

y = (18.8 - -x) / (thirty - -10)

y = 28.viii / 40

y = 0.72

You lot can see that if an x value is provided that is outside the bounds of the minimum and maximum values, that the resulting value will non be in the range of 0 and 1. You could check for these observations prior to making predictions and either remove them from the dataset or limit them to the pre-divers maximum or minimum values.

Y'all can normalize your dataset using the scikit-larn object MinMaxScaler.

Good practice usage with the MinMaxScaler and other rescaling techniques is as follows:

Fit the scaler using available training data. For normalization, this ways the training information will exist used to estimate the minimum and maximum observable values. This is done by calling the fit() function,
Apply the calibration to training data. This ways you lot can use the normalized data to railroad train your model. This is done past calling the transform() role
Apply the calibration to data going frontward. This ways you lot can prepare new data in the futurity on which you lot desire to brand predictions.

If needed, the transform can be inverted. This is useful for converting predictions dorsum into their original calibration for reporting or plotting. This tin be done by calling the inverse_transform() function.

Beneath is an example of normalizing the Minimum Daily Temperatures dataset.

The scaler requires data to exist provided every bit a matrix of rows and columns. The loaded time series data is loaded as a Pandas Series. Information technology must then be reshaped into a matrix of one column with iii,650 rows.

The reshaped dataset is then used to fit the scaler, the dataset is normalized, then the normalization transform is inverted to prove the original values once more.

three

four

seven

xviii

# Normalize fourth dimension series information

from pandas import read_csv

from sklearn . preprocessing import MinMaxScaler

# load the dataset and print the first 5 rows

series = read_csv ( 'daily-minimum-temperatures-in-me.csv' , header = 0 , index_col = 0 )

print ( serial . head ( ) )

# fix data for normalization

values = series . values

values = values . reshape ( ( len ( values ) , 1 ) )

# train the normalization

scaler = MinMaxScaler ( feature_range = ( 0 , 1 ) )

scaler = scaler . fit ( values )

impress ( 'Min: %f, Max: %f' % ( scaler . data_min_ , scaler . data_max_ ) )

# normalize the dataset and impress the showtime five rows

normalized = scaler . transform ( values )

for i in range ( v ) :

print ( normalized [ i ] )

# inverse transform and print the first v rows

inversed = scaler . inverse_transform ( normalized )

for i in range ( 5 ) :

print ( inversed [ i ] )

Running the example prints the first 5 rows from the loaded dataset, shows the same 5 values in their normalized form, so the values back in their original scale using the inverse transform.

We tin can also see that the minimum and maximum values of the dataset are 0 and 26.3 respectively.

iii

five

Date

1981-01-01 xx.seven

1981-01-02 17.ix

1981-01-03 18.8

1981-01-04 14.half-dozen

1981-01-05 fifteen.8

Name: Temp, dtype: float64

Min: 0.000000, Max: 26.300000

[ 0.78707224]

[ 0.68060837]

[ 0.7148289]

[ 0.55513308]

[ 0.60076046]

[ twenty.7]

[ 17.9]

[ eighteen.8]

[ 14.6]

[ 15.8]

In that location is another type of rescaling that is more robust to new values existence exterior the range of expected values; this is called Standardization. We will look at that next.

Standardize Time Series Data

Standardizing a dataset involves rescaling the distribution of values so that the hateful of observed values is 0 and the standard departure is i.

This can exist idea of as subtracting the mean value or centering the data.

Similar normalization, standardization can be useful, and even required in some machine learning algorithms when your time series information has input values with differing scales.

Standardization assumes that your observations fit a Gaussian distribution (bong curve) with a well behaved mean and standard divergence. You can still standardize your fourth dimension series data if this expectation is not met, but you may non get reliable results.

This includes algorithms like Back up Vector Machines, Linear and Logistic Regression, and other algorithms that assume or have improved performance with Gaussian data.

Standardization requires that you know or are able to accurately estimate the mean and standard departure of observable values. You may be able to estimate these values from your training data.

A value is standardized every bit follows:

y = (ten - mean) / standard_deviation

Where the mean is calculated as:

And the standard_deviation is calculated every bit:

standard_deviation = sqrt( sum( (x - mean)^2 ) / count(x))

For example, nosotros can plot a histogram of the Minimum Daily Temperatures dataset as follows:

from pandas import read_csv

from matplotlib import pyplot

serial = read_csv ( 'daily-minimum-temperatures-in-me.csv' , header = 0 , index_col = 0 )

series . hist ( )

pyplot . show ( )

Running the code gives the following plot that shows a Gaussian distribution of the dataset, as assumed by standardization.

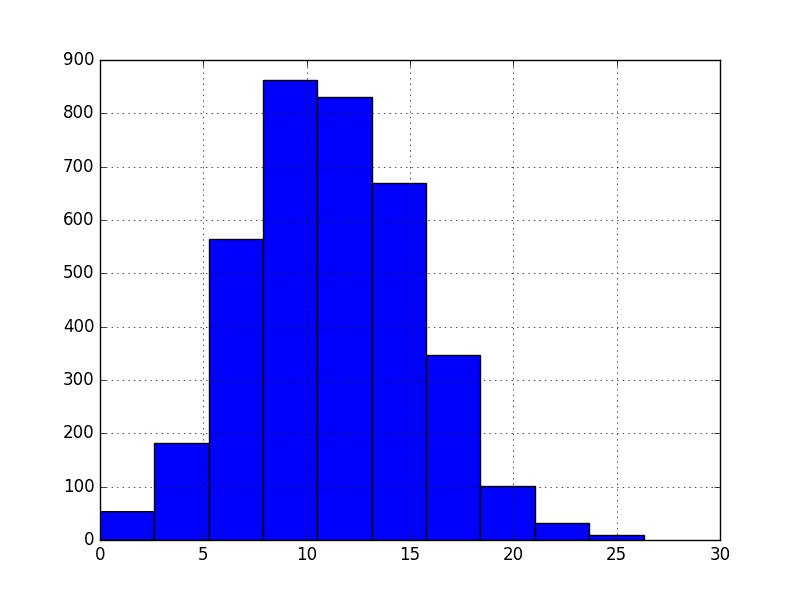
Minimum Daily Temperatures Histogram

We can guesstimate a mean temperature of 10 and a standard divergence of about 5. Using these values, we tin standardize the first value in the dataset of xx.7 equally follows:

y = (x - hateful) / standard_deviation

y = (20.7 - x) / 5

y = (10.7) / 5

y = two.14

The mean and standard divergence estimates of a dataset can be more robust to new data than the minimum and maximum.

Y'all tin can standardize your dataset using the scikit-larn object StandardScaler.

Below is an case of standardizing the Minimum Daily Temperatures dataset.

iii

five

eight

fourteen

xvi

nineteen

# Standardize time serial data

from pandas import read_csv

from sklearn . preprocessing import StandardScaler

from math import sqrt

# load the dataset and print the first 5 rows

series = read_csv ( 'daily-minimum-temperatures-in-me.csv' , header = 0 , index_col = 0 )

print ( series . caput ( ) )

# prepare data for standardization

values = series . values

values = values . reshape ( ( len ( values ) , 1 ) )

# railroad train the standardization

scaler = StandardScaler ( )

scaler = scaler . fit ( values )

print ( 'Hateful: %f, StandardDeviation: %f' % ( scaler . mean_ , sqrt ( scaler . var_ ) ) )

# standardization the dataset and print the outset 5 rows

normalized = scaler . transform ( values )

for i in range ( 5 ) :

print ( normalized [ i ] )

# inverse transform and print the first 5 rows

inversed = scaler . inverse_transform ( normalized )

for i in range ( v ) :

print ( inversed [ i ] )

Running the example prints the offset five rows of the dataset, prints the same values standardized, then prints the values back in their original scale.

We can encounter that the estimated mean and standard deviation were 11.ane and iv.0 respectively.

iii

fifteen

sixteen

Date

1981-01-01 20.7

1981-01-02 17.ix

1981-01-03 eighteen.8

1981-01-04 14.6

1981-01-05 15.8

Proper name: Temp, dtype: float64

Mean: 11.177753, StandardDeviation: 4.071279

[ 2.33888328]

[ 1.65113873]

[ 1.87219948]

[ 0.84058266]

[ 1.13533032]

[ 20.7]

[ 17.nine]

[ eighteen.eight]

[ fourteen.half dozen]

[ fifteen.8]

Summary

In this tutorial, yous discovered how to normalize and standardize fourth dimension series information in Python.

Specifically, you learned:

That some machine learning algorithms perform better or even crave rescaled data when modeling.
How to manually calculate the parameters required for normalization and standardization.
How to normalize and standardize time serial data using scikit-learn in Python.

Exercise you have any questions near rescaling fourth dimension series data or about this mail?
Ask your questions in the comments and I will practice my all-time to respond.

Want to Develop Time Series Forecasts with Python?

Develop Your Ain Forecasts in Minutes

...with just a few lines of python code

Find how in my new Ebook:
Introduction to Time Series Forecasting With Python

It covers self-study tutorials and end-to-end projects on topics like: Loading data, visualization, modeling, algorithm tuning, and much more than...

Finally Bring Time Series Forecasting to
Your Own Projects

Skip the Academics. But Results.

See What's Inside